在反比例函数y=-(k为常数且k≠0)中，比例系数k具备一定的几何意义：

　　如图，点P是双曲线y=-(k为常数且k≠0)上任意一点，过P作PM⊥x轴于M，作PN⊥y轴于N。设点P的坐标为(x，y)，则PM=|y|，PN=|x|。

　　S四边形PMON=PM·PN=|x|·|y|=|xy|

　　∵y=- ∴xy=k ∴S=|k|

　　即过双曲线上任意一点分别作坐标轴的垂线，所得矩形面积为|k|。

　　也就是说矩形的形状随着P点的变化而变化，但面积始终是定值。利用这一结论我们可以解决一系列的问题。

　　例1.如图：点C是x轴正半轴上动点，过C作x轴的垂线，交双曲线 y=-于点B，过B作y轴的垂线交y轴于D，当C沿x轴的正向运动时，

　　(1)四边形DOCB的面积如何变化？

　　[解答]：面积不发生变化，S=|k|=1。

　　(2)三角形BOD的面积为_____

　　[解答]：S△BOC=-

　　(3)过BO的直线与双曲线的另一交点为B’，此时三角形B’CB的面积为_____。

　　[解答]：S△BB’C=|k|=1

　　(4)过B’作B’F⊥x轴于F，连接BF，则平行四边形FB’CB的面积为_____

　　[解答]：S四边形FB’CB=|2k|=2

　　(5)如图过B’作B’E⊥y轴于E，连接CE，则四边形B’ECB的面积为______。

　　[解答]：S四边形BB’EC=-=-

　　(6)如图，作B’F⊥x轴，BD⊥y轴，连接DF、CE，则六边形FB’ECBD的面积为______

　　[解答]：S六边形FB’ECBD=3|k|=3

　　例2.如图：在平面直角坐标系中,A为y轴正半轴上的一点，过A作x轴的平行线，交函数y=--(x<0)的图像于B，交函数y=-(x>0)的图像于C，过C作y轴的平行线交BO的延长线于D。

　　(1)如果点A的坐标为(0，2)，求线段AB与线段CA的长度之比。

　　(2)如果点A的坐标为(0，a)，求线段AB与线段CA的长度之比。

　　(3)在(2)的条件下,求四边形AODC的面积。

　　[分析]：要求解的图形面积为直角梯形的面积，因此需要先确定图中A、O、C、D四个点的点坐标，进而求出上底AO、下底CD、高AC的长度。其中D点的确定则需要求直线BO的解析式。

　　[解答]：(1)由A(0，2)得出B(-1，2)、C(3，2)即AB=1，AC=3

　　(2)由A(0，a)得出B(--，a)，C( -，a)，AB=-，AC=-，AB：AC=1：3

　　(3)直线BC的解析式：

　　y=--，D(-，-3a)

　　SAODC=(a+4a)(-)(-)=15

　　例3.如图，在反比例函数y=-(x>0)的图像上有点A、B、C、D，它们的横坐标依次为1、2、3、4，分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S1、S2、S3，则S1+S2+S3的值是多少？

　　[分析]：将面积为S2、S3的图形左移拼凑成一个大的矩形，求解这个矩形的面积。

　　[解答]：如图：S1+S2+S3=AG·GE=1×（2--)=-

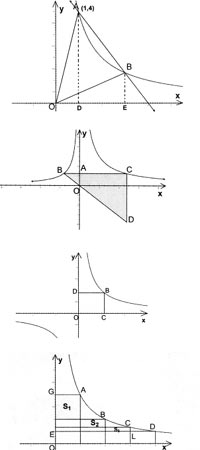
　　例4.如图，在平面直角坐标系xOy中，一次函数y=k1x+b的图像与反比例函数y=-的图像交于A(1，4)、B(3，m)两点，求△AOB的面积。

　　[分析]将此三角形的面积转化为直角梯形的面积进行求解。

　　[解答]

　　∵A(1，4)在反比例函数y=-图像上，∴k2=4，即y=-，B(3，-)，过A、B分别作AD⊥x轴，BE⊥x轴，A、B都在双曲线上，∴S△AOD=S△BOE=-=2

　　S△AOB=S四边形AOEB-S△BOE

　　=S△AOD+S梯形ADEB-S△BOE

　　=S梯形ADEB

　　=(AD+BE)·■=(4+-)·■=-(周五继续刊登)