|
班级____________姓名______________ 学号____________
一、选择题(共12小题,每小题5分,共60分)
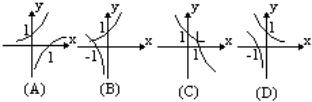
1、已知a>0,a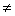 0,函数y=ax与y=loga(-x)的图象只能是 ( ) 0,函数y=ax与y=loga(-x)的图象只能是 ( )
 翰林汇 翰林汇
2、函数y=ax2-2ax+2+b(a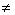 0)在[2,3]上有最大值5及最小值2,则a,b的值为( ) 0)在[2,3]上有最大值5及最小值2,则a,b的值为( )
(A)a=1,b=0 (B)a=-1,b=3
(C)a=1,b=0或a=-1,b=3 (D)以上都不对翰林汇
3、定义在(-∞,+∞)上的任意函数f(x)都可以表示为一个奇函数g(x)和一个偶函数h(x)之和,如果 f(x)=lg(10x+1),x∈(-∞,+∞),那么 ( )
(A)g(x)=x,h(x)=lg(10x+10-x+2) (B)g(x)=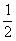 [lg(10x+1)+x],h(x)= [lg(10x+1)+x],h(x)=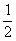 [lg(10x+1)-x] [lg(10x+1)-x]
(C)g(x)= ,h(x)= lg(10x+1)- ,h(x)= lg(10x+1)-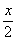 (D)g(x)= (D)g(x)=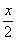 ,h(x)=lg(10x+1)+ ,h(x)=lg(10x+1)+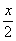 翰林汇 翰林汇
4、函数f(x)=ax-b-1(a>0,a≠1)图像只在第一、三、四象限.则 ( )
(A)a>1,b∈R (B)0<a<1,b>0 (C)0<a<1,b∈R (D)a>1,b>0翰林汇
5、当x∈(1,+∞)时,函数y=xa的图像恒在直线y=x的下方,则a的取值范围是( )
(A)a<1 (B)0<a<1 (C)a>0 (D)a<0翰林汇
6、图中三条对数函数图像,若a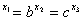 >1,则x1、x2、x3的大小关系是( ) >1,则x1、x2、x3的大小关系是( )
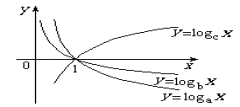
(A)x1>x2>x3 (B)x3>x2>x1 (C)x3>x1>x2 (D)x2>x1>x3翰林汇
7、将函数y=f(x)的图像沿x轴向左平移一个单位,再沿y轴翻折180o,得到y=lgx的图像,则f(x)的解析式为 ( )
(A)f(x)=lg(1+x) (B)f(x)=lg[-(x+1)] (C)f(x)=lg(1-x) (D)f(x)=-lg(1-x)翰林汇
8、△ABC中,角A、B、C的对边分别记为a、b、c(b≠1),且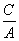 、 、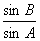 都是方程log 都是方程log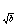 x=logb(4x-4)的根,则△ABC ( ) x=logb(4x-4)的根,则△ABC ( )
(A)是等腰三角形但不是直角三角形 (B)是直角三角形但不是等腰三角形
(C)是等腰直角三角形 (D)不是等腰三角形,也不是直角三角形翰林汇
9、把函数y=f(x)在x∈[a,b]之间的一段图像近似地看作线段(如图),设a<m<b,则f(m)的近似值表示为 ( )
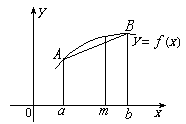
(A)f(a)+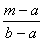 [f(b)-f(a)] (B)f(b)- [f(b)-f(a)] (B)f(b)-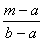 [f(b)-f(a)] [f(b)-f(a)]
(C) [f(a)+f(b)] (D) [f(a)+f(b)] (D) 翰林汇 翰林汇
10、已知函数f(x)的图像是C1,函数y=C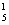 x4+C x4+C x3+C x3+C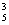 x2+C x2+C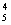 x+x5的反函数为g(x),若g(x)的图像C2与C1关于y轴对称,则f(x)的解析式为 ( ) x+x5的反函数为g(x),若g(x)的图像C2与C1关于y轴对称,则f(x)的解析式为 ( )
(A)y=1-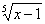 (B)y=1- (B)y=1-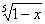 (C)y= (C)y=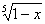 -1 (D)y= -1 (D)y=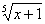 -1翰林汇 -1翰林汇
11、将函数y=2x的图像向左平移一个单位得图像C1,再将C1向上平移一个单位得到图像C2,作出C2关于直线y=x的对称图像C3,则C3的解析式是 ( )
(A)y=log2(x+1)+1 (B)y=log2(x+1)-1
(C)y=log2(x-1)+1 (D)y=log2(x-1)-1翰林汇
12、定义在区间(-∞,+∞)的奇函数f(x)为增函数,偶函数g(x)在区间[0,+∞)的图像与f(x)的图像重合,设a>b>0,给出下列各式:
①f(b)-f(-a)>g(a)-g(-b); ②f(b)-f(-a)<g(a)-g(-b);
③f(a)-f(-b)>g(b)-g(-a); ④f(a)-f(-b)<g(b)-g(-a).
其中正确的是 ( )
(A)①与④ (B)②与③ (C)①与③ (D)②与④翰林汇
二、填空题(每小题4分,满分16分)
13、函数y=lg(5x+7)的反函数是_____,反函数的值域是_____。翰林汇
14、函数y=x·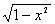 的最大值是________。翰林汇 的最大值是________。翰林汇
15、使x2>x3成立的x的取值范围是_______翰林汇
16、函数y=x-2+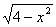 的最小值是________;最大值是________. 的最小值是________;最大值是________.
班级____________姓名______________ 学号____________
翰林汇
一、选择题答题卡
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题
13 , ;14 ;
15 ;16 , .
三、解答题(共6小题,满分74分)
17、(满分12分)求下列函数的定义域并判断其奇偶性:
(1)f(x)=lg(x-1)+lg(x+1); (2)f(x)=(x-1)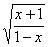 (|x|<1) (|x|<1)
翰林汇
18、(满分12分)已知函数f(x)=( eq f(x-1,x+1) )2(x≥1),f-1(x)为f(x)的反函数
(1)求f-1(x)的定义域和单调区间;(2)求g(x)= eq f(1,f-1(x)) + eq (x) +2的最小值. eq f(1,f-1(x))
翰林汇
19、(满分12分)已知f(x)=x2+(lga+2)x+lgb,且f(-1)=-2,若f(x)≥2x对于任意x∈R恒成立,
(1)求a,b的值;(2)指出f(x)的奇偶性并判断f(-4)与f(-1)的大小.
20、(满分13分)设A={x|1<x<3},集合B是关于x的不等式组 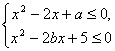 的解集.试确定a,b的取值范围,使得A 的解集.试确定a,b的取值范围,使得A B. B.
翰林汇
21、(满分13分)解下列方程:
(1)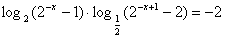 ;(2) ;(2)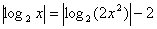 . .
翰林汇
22、(满分12分)已知函数f(x)在R+上有定义,且具有如下性质:
① f(x+y)=f(x)+f(y); ② 若f(x)≥f(y),则x≥y; ③ f(2)=1,
(1)求f(1)、f(4)的值; (2)若f(x)+f(x+3)≤2,求x的范围。 |
